The researchers managed the challenge of quantification, simulation, and weight appointment to counterfactuals and diversely heterogeneous sets of factors accountable for the dynamism of malaria transmission to anticipate robust circumstance-specific policy advice for malaria control. The modular framework aspires to extend the Ross-Macdonald model and previous mathematical models for mosquito-borne pathogens by orienting overwhelming computational, conceptual, and parametric complexity originating from combining all dimensions, interactions, and factors associated with the parasite Plasmodium falciparum, their dispersal, contexts, and malarial hosts and vectors.
This novel patch-based differential equation framework bridges two relatively contradictory but well-established views of malaria. One supposition is that local ecology molds human malaria transmission to such an extent that preventive measures taken in one place or time are very unlikely to be effective elsewhere. Another view, based on the Ross-Macdonald model, is that malaria transmission intensity can be quantified using a small set of bionomic parameters. The abridged modeling version should be able to acknowledge the contextual, multifactorial, and non-linear nature of malaria dissemination dynamics. The patch-based framework offers flexibility and scalability.
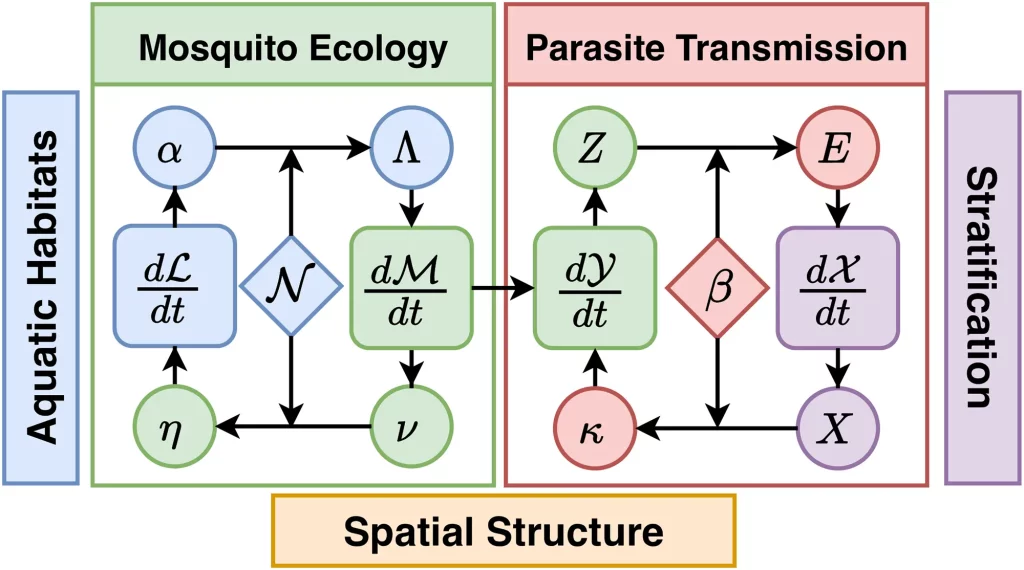
Image Source: https://doi.org/10.1371/journal.pcbi.1010684
Accommodating Heterogeneity for Capturing Dynamism
The framework has been designed to investigate the spatial transmission dynamics of malaria in a geographical area called the spatial domain. The structural elements, the Patches, were designed to be flexible enough to handle arbitrary human population residency patterns, stratification, etc. The spatial domains were subdivided to accommodate diverse locations and mosquito ecology, including the places where human stays, where mosquitoes feed blood, and the aquatic habitat where they lay eggs. The model accommodates population strata such as residency, immunity, behaviors affecting the risk of disease, and epidemiologically relevant factors. Membership matrices were created to devise interactions among different structural elements or patches.
Researchers created a Time Spent (TiSp) matrix and a Time At Risk (TaR) matrix to elucidate exposure to the risk of mosquito bites due to human movement patterns. An intermediate quantity of ambient population density was calculated and integrated with the matrices to accurately determine the available population for blood feeding while taking into account human behavior, mosquito biting rates, and other preferences. Moreover, the researchers also considered other important aspects such as human blood-feeding fractions, parasite transmission, Entomological inoculation rate, etc. To depict mosquito population dynamics, the researchers formulated algorithms for egg deposition rates and egg-laying distributions. For instance, they formulated an egg distribution matrix to model egg distribution among habitats.
Furthermore, the researchers computed parasite dispersal factors. A mosquito tracking matrice is used to follow parasite dispersal in mosquitoes. They derived a human transmitting capacity distribution (HTCD) matrix from comprehending parasite dispersal by humans. The HTCD matrix employs the biting distribution matrix to count from the infectious bite and weight biting appropriately for the next blood feeding. Since transmission requires two bites, they used the TaR matrix to determine where a human becomes infected and where it infects a mosquito. They take into account the distances of distribution of the parasite and average reproduction success rates of the parasite to gain insight into the strategy for malaria outbreak control. They described the endemic reproductive number, which denotes potential transmission affected by the immune system.
The researchers defined adjusted reproductive numbers to describe a population with no acquired immunity adjusted by malaria control. The adjusted reproductive number represents a threshold for malaria transmission, whether the transmission will occur locally or become endemic. The next-generation matrix was computed to evaluate whether infections were transmitted from a single mosquito to humans or infected humans to mosquitoes and how many humans could be infected by one mosquito.
Core Dynamical Components
The framework possesses state-space models of four core dynamical components: aquatic mosquito ecology, adult mosquito ecology, infection dynamics, infection, and immunity. The first core dynamical component consists of the algorithm that computes mosquito survival and development to adults from eggs laid. For aquatic population dynamics, the researchers integrated a previously published model. The second core dynamical component represents adult mosquito ecology. The algorithms describe adult mosquito mortality and dispersal. It includes another important factor of mosquito mobility.
The third core dynamical component represents parasite infection dynamics in adult mosquito populations. The researchers integrated a previously published delay differential equation for the density of infectious mosquitoes to include space and a time-varying extrinsic incubation period (EIP). The fourth core dynamical component describes parasite infection dynamics in human populations.
Conclusion
The modular framework offers a realistic model, conjugating a century of research and cases. The new algorithms simulate adult mosquito demography and egg laying. The matrices for parasite dispersal, local reproductive numbers, malaria connectivity, and re-examination of entomological inoculation rates and human biting rates will certainly be impactful towards generating more specialized and robust malaria control policies and dealing with uncertainty because each structural element, ‘patches,’ can accommodate higher variability, offer flexibility, and adaptability.
The overall framework is useful for analyzing the spatial transmission dynamics of the disease. The researchers anticipate that the framework can be effectively utilized for studying malaria in a place and can be implemented to support malaria disease control national programmatic activities. A software package is also available to implement the framework. The model can be utilized to identify differences in transmission patterns in different landscapes and thus help control programs to decide suitable drugs and medical attention to populations, formulate rules & regulations, and outreach programs and initiatives to control vector or larval propagation. The scientists proposed that they would endeavor to address temporal dimensions such as the effects of seasons and weather and planned to utilize the model to generate policy advice for Bioko Islands.
Article Source: Reference Paper
Learn More:
Aditi is a consulting scientific writing intern at CBIRT, specializing in explaining interdisciplinary and intricate topics. As a student pursuing an Integrated PG in Biotechnology, she is driven by a deep passion for experiencing multidisciplinary research fields. Aditi is particularly fond of the dynamism, potential, and integrative facets of her major. Through her articles, she aspires to decipher and articulate current studies and innovations in the Bioinformatics domain, aiming to captivate the minds and hearts of readers with her insightful perspectives.










