In the world of drug discovery, predicting how well a drug molecule will bind to its target is like figuring out the best path on a treasure map when you’re lost. Scientists use complex calculations to predict this binding affinity. One powerful method is called “Absolute Binding Free Energy” (ABFE) calculations. These calculations help scientists understand how strongly a drug molecule will stick to its target, which is crucial for designing effective drugs.
To make this process faster and easier, researchers from Cambridge, Newcastle University, and the University of Edinburgh have developed a new, fully automated ABFE workflow. This workflow is like a smart assistant that helps scientists navigate the treasure map more efficiently, reducing the time and effort needed to find the treasure.
Introduction
The prediction of drug binding affinity to its target is very important in early-stage drug discovery. Free energy calculations, based on molecular dynamics or Monte Carlo sampling, are recommended as the optimal method for predicting these affinities. While relative binding free energy (RBFE) calculations are commonly used, they are limited to structurally similar molecules binding to the same target with the same binding mode. Absolute binding free energy calculations overcome these constraints by removing a single ligand’s intermolecular interactions in bound and unbound states. This makes ABFE calculations applicable to a wider range of problems.
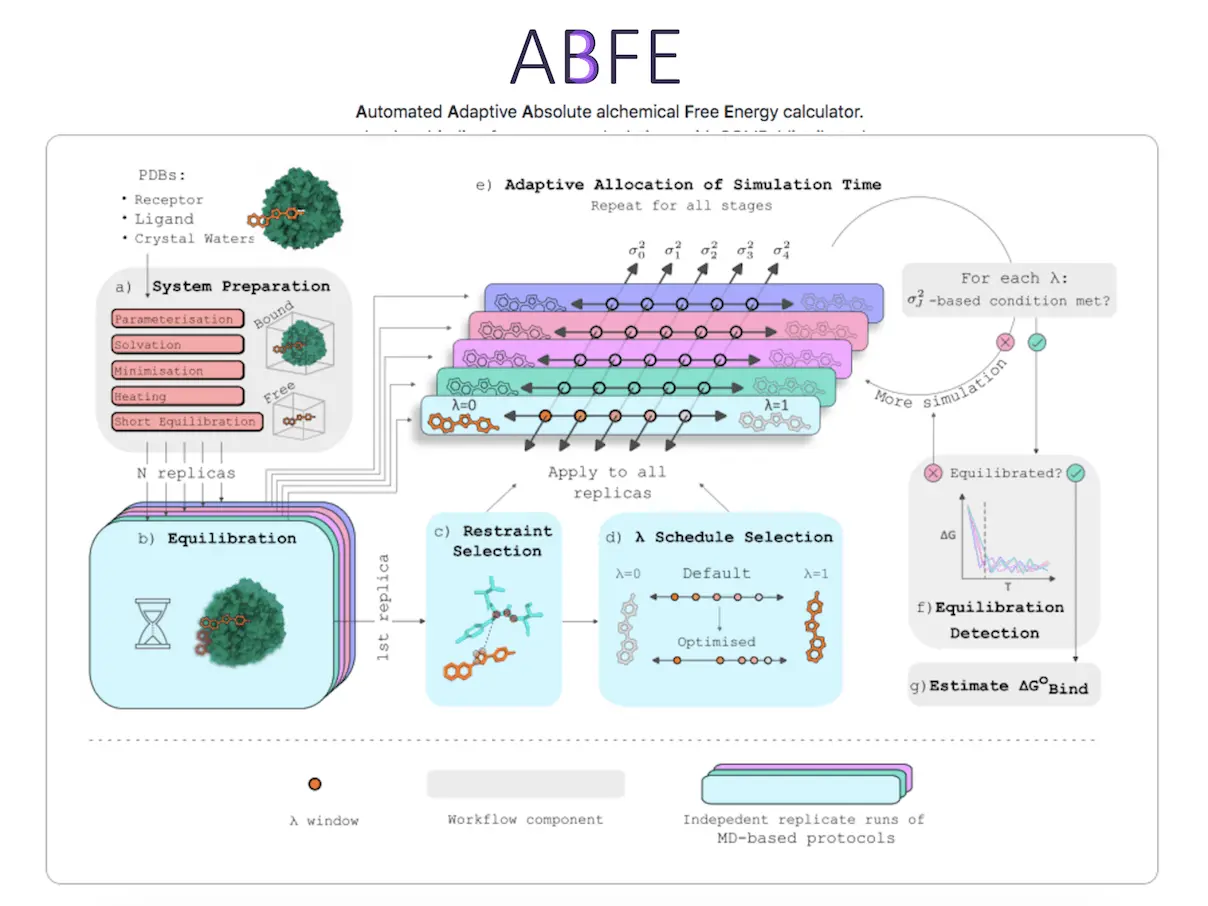
However, ABFE calculations are computationally expensive due to the need for extensive sampling and are susceptible to sampling issues like slow rehydration of the binding site and side-chain rearrangement. Efficient automated ABFE workflows are required to reduce both computational cost and human intervention. This study presents a fully automated ABFE workflow that includes automated selection of λ windows, ensemble-based detection of equilibration, and adaptive allocation of sampling time based on inter-replicate statistics.
Theory and Methodology
Selection of Intermediate States
Optimal intermediate states minimize the standard error of the overall free energy estimate for a given total sampling time. Intermediate states, controlled by a variable λ, are necessary because sampling only at the end-states of interest is insufficient. The Bennett Acceptance Ratio (BAR) or Zwanzig equation requires intermediate states for accurate estimates.
Allocation of Sampling Time
The optimal allocation of sampling time is crucial, especially when few states have a much higher computational cost per independent sample. Adaptive allocation of simulation time can accelerate equilibration and improve efficiency.
Detection of Equilibration and Convergence
Equilibration detection is necessary to discard samples from initial transients, which could bias the final free energy estimate. Convergence assessment ensures that the simulation data represents the underlying stationary distributions accurately.
Key Equations and Concepts
Free Energy Change Estimate:
This concept involves integrating the mean gradient of the Hamiltonian (a function describing the total energy of the system) with respect to a parameter λ, over the entire path from λ=0 to λ=1. It basically calculates the difference in free energy between two states by averaging the changes in energy along the way.
Variance of the Estimated Free Energy Change:
This concept involves calculating the variance (a measure of how much the data spreads out) of the estimated free energy change. The variance depends on the number of uncorrelated samples taken at each intermediate state and the variability in the energy gradient at those states. A higher number of uncorrelated samples and lower variance in the energy gradient lead to a more accurate free energy estimate.
Optimizing Sampling Time Allocation:
This involves distributing the total available sampling time in a way that optimizes the efficiency of the calculations. It takes into account the statistical inefficiency (how quickly the samples become uncorrelated), the total sampling time, and a Lagrangian multiplier (a parameter used to find the optimal solution). The goal is to allocate more time to states that are harder to sample accurately, ensuring that the overall calculation is as efficient and accurate as possible.
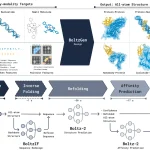
Automated Workflow
The automated ABFE workflow implemented in the open-source package A3FE includes the following:
Automated Selection of λ Windows:
The workflow uses an adaptive algorithm to select intermediate states with consistent overlap, ensuring robust and simple implementation.
Ensemble-Based Detection of Equilibration:
Equilibration is detected using a paired t-test between free energy estimates at initial and final portions of an ensemble of runs, ensuring reliable detection.
Adaptive Allocation of Sampling Time:
Sampling time is allocated based on inter-replicate statistics, optimizing the allocation to improve efficiency and reduce computational costs.
Conclusion
The automated ABFE workflow demonstrated in this study is rapid, robust, and easy to implement. It shows equivalent results to non-adaptive schemes while often accelerating equilibration. The workflow, implemented in A3FE, significantly reduces computational costs and human intervention, unlocking the potential of ABFE calculations in drug discovery. The use of adaptive algorithms and ensemble-based metrics enhances the robustness and efficiency of ABFE calculations, making them more accessible and practical for a wider range of applications.
Article Source: Reference Paper | The complete workflow is implemented in the open-source package A3FE, which is available on GitHub.
Important Note: ChemRxiv releases preprints that have not yet undergone peer review. As a result, it is important to note that these papers should not be considered conclusive evidence, nor should they be used to direct clinical practice or influence health-related behavior. It is also important to understand that the information presented in these papers is not yet considered established or confirmed.
Follow Us!
Learn More:
Neermita Bhattacharya is a consulting Scientific Content Writing Intern at CBIRT. She is pursuing B.Tech in computer science from IIT Jodhpur. She has a niche interest in the amalgamation of biological concepts and computer science and wishes to pursue higher studies in related fields. She has quite a bunch of hobbies- swimming, dancing ballet, playing the violin, guitar, ukulele, singing, drawing and painting, reading novels, playing indie videogames and writing short stories. She is excited to delve deeper into the fields of bioinformatics, genetics and computational biology and possibly help the world through research!