To estimate cell-to-cell heterogeneity in non-Markovian signaling systems, mathematicians from The Korea Advanced Institute of Science and Technology (KAIST) and Institute for Basic Science (IBS), Korea, devised a Bayesian inference approach. The approach could aid in the development of treatments that kill pathogenic or cancerous cells.
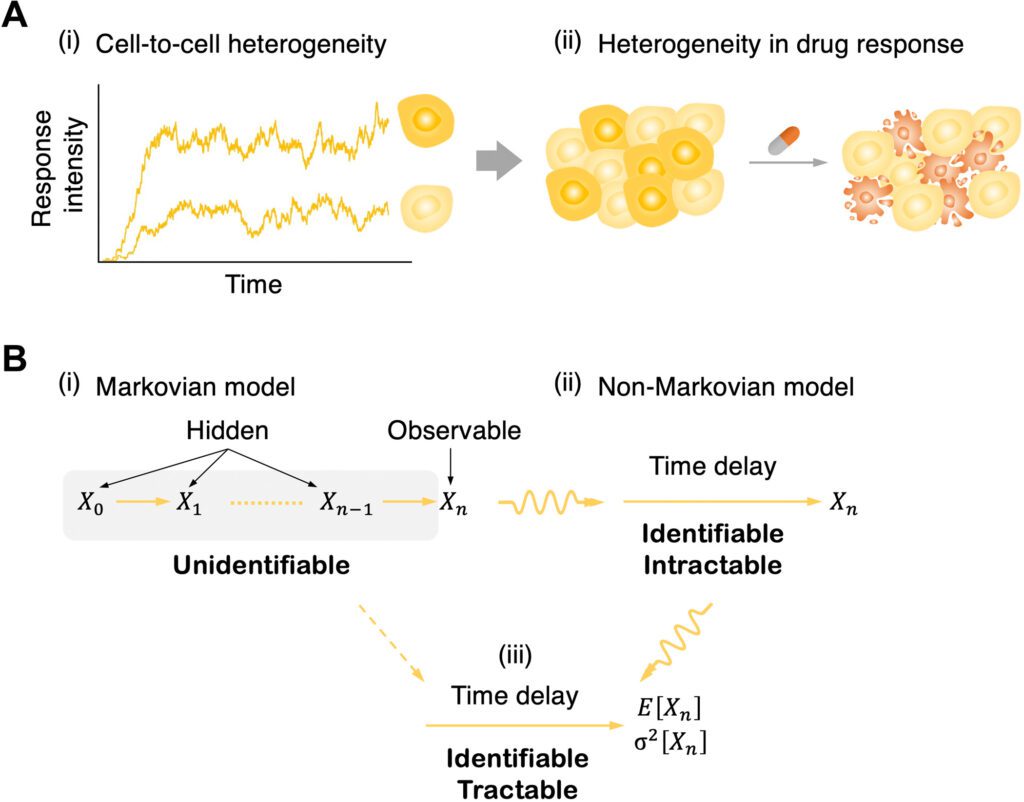
Image Source: Systematic inference identifies a major source of heterogeneity in cell signalling dynamics: The rate-limiting step number.
Recognizing the source of cell-to-cell variability in cell signaling dynamics is fundamental to understanding drug response variability and developing potent therapeutics. Be that as it may, it is challenging because not all signalling intermediate reactions can be experimentally estimated simultaneously.
This can be overcome by supplanting them with a single random time delay, but the subsequent cycle is non-Markovian, making it challenging to derive cell-to-cell heterogeneity in reaction rates and time delays.
To address this, the scientists fostered an effective and scalable moment-based Bayesian inference method (MBI) with an easy-to-use computational package that inferred cell-to-cell heterogeneity in the non-Markovian signaling interaction.
They applied MBI to single-cell expression profiles from promoters responding to antibiotic agents and found a significant source of cell-to-cell variability in antibiotic stress response or the number of rate-limiting steps in signaling cascades. This information can assist with distinguishing effective therapies that can destroy pathogenic or cancer cells, and the methodology can be applied to precision medicine.
Sources of Cell Signaling Heterogeneity and Avoiding Constraints in the Process
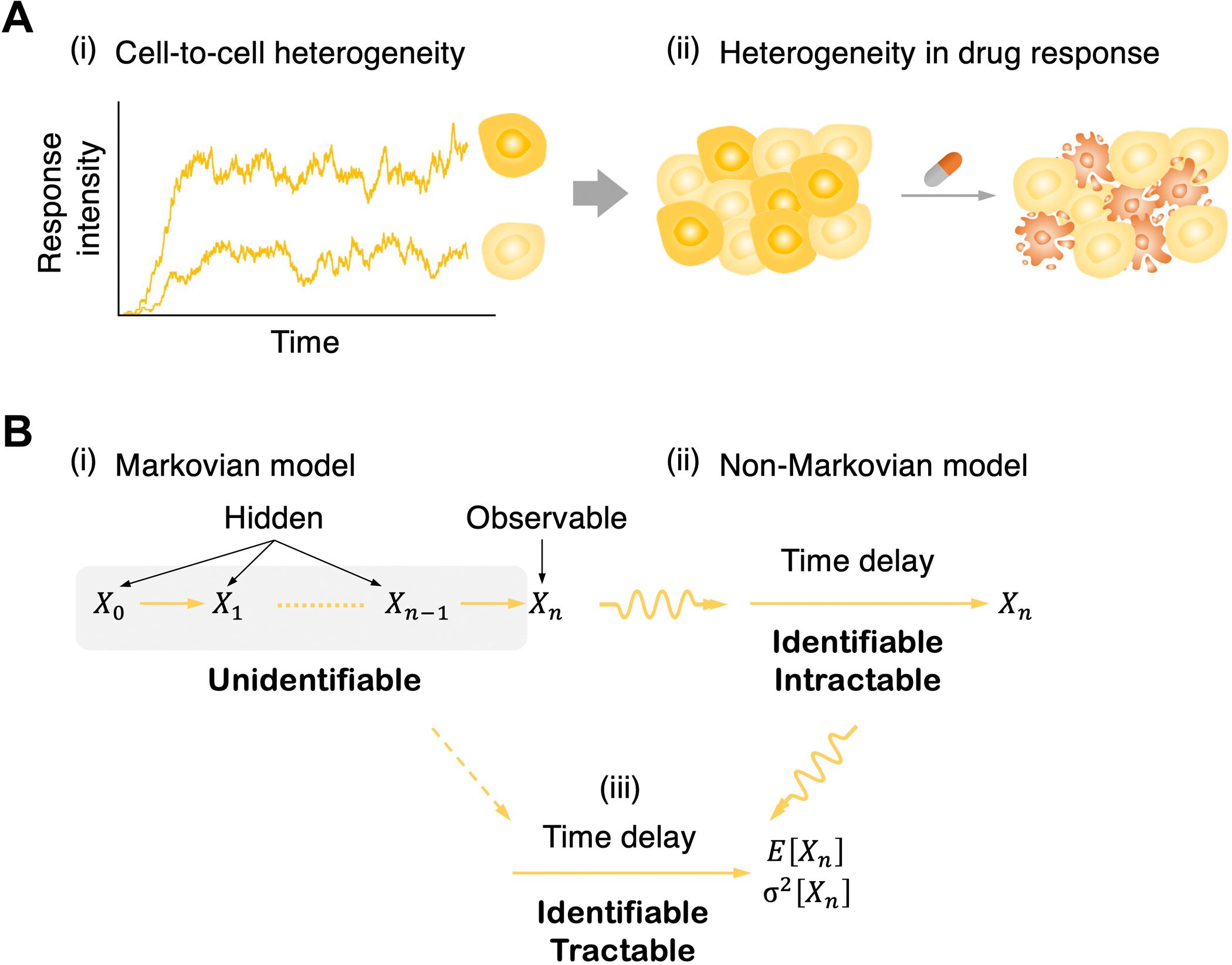
The response of genetically identical cells to the equivalent extracellular signal is generally heterogeneous in both response time and strength, even in a homogeneous environment. This cell signaling heterogeneity, at last, prompts diverse, frequently unpredictable clinical complications, like drug response variability, the emergence of persister cells, incomplete penetrance, and phenotypic plasticity.
One of the significant sources of this cell-signaling heterogeneity is a distinction in cell phenotypes, like cell cycle phase, cell growth rate, or asymmetric cell division. One more significant source is heterogeneity in the signal cascades, like the quantity of signaling receptors and the kinetics of various intermediate signaling responses.
In any case, while cellular phenotypes can be followed with flow cytometry, microfluidics, furthermore time-lapse microscopy, a couple of steps of signaling cascades can, for the most part, be followed in a single cell, for instance, with multicolor luciferase reporter assays. On account of this constraint of the information, intermediate signaling kinetics are unidentifiable.
One promising method for avoiding this is to supplant a chain of hidden intermediate steps with a single random time delay. This permits one to portray signaling cascades with a chain of hidden steps by utilizing a straightforward delayed birth-death process; it is discernible to have just a single variable that tentatively: birth (i.e., signal enactment), delay (i.e., signal transduction), and death (i.e., decay of observable signaling particles).
In any case, since the model was non-Markovian (i.e., the formation of the response molecule relies upon past signal activation occasions because of a time delay as well as the present status of a system), deeply grounded inference machinery given the Markov property (i.e., memoryless; the formation of the response particle relies just upon the present status, not on the past) can’t be straightforwardly applied.
The Moment Based Bayesian Inference Methodology
As of late, significant headway has been made: A Bayesian inference methodology in light of non-Markovian delay chemical master equations (CMEs) depicting the time evolution of stochastic frameworks with a delay has been developed. In any case, this framework lies with the assumption that all-time trace measurements are acquired from identical cells with equivalent biochemical parameters, and consequently, measuring the heterogeneity can’t be utilized in signaling parameters (e.g., signal transduction delay) across cells.
This challenge can be overwhelmed with a mixed-effects modeling approach that offers a framework to analyze cell population-level data and records for cell-to-cell heterogeneity in the population. Be that as it may, its actual capacity in non-Markovian delayed systems still can’t be understood.
The other constraint of the past techniques given CMEs is computational intractability. Since they track entire probabilities over the integer-valued state space of molecule counts, inference utilizing them significantly slows down when the amount of provided data increases.
One potential solution for this may be to utilize low-order moments of data (e.g., mean) rather than all the individual data points. In particular, following the mean number of molecules, which incorporates the fundamental data for determining the model parameters, doesn’t increase the amount of data utilized for parameter estimation and, in this way, computational cost, albeit the quantity of measurements (i.e., total data points) increases.
Notwithstanding, deduction of definite moments is challenging in non-Markovian delayed models as the conditional probabilities, portraying the impact of the models’ history (i.e., past model dynamics) on the current model dynamics, should be taken care of. Hence, the approximate moments have been utilized under the presumption that the quantity of molecules is huge.
Here, the scientists fostered an exact moment-based Bayesian inference methodology (MBI) for signaling processes of a heterogeneous cell population by utilizing a mixed-effects modeling approach and determining the exact moments of the process. It can precisely capture the cell-to-cell heterogeneous birth and death rates and delays for signal transduction and feedback.
Besides, MBI can be applied to vast amounts of information as it utilizes just the first moments of enormous information rather than all individual data points.
The researchers utilized MBI to previously published single-cell profiles of time-lapse fluorescent protein expression from different promoters in light of four antibiotic stresses: tetracycline (TET), trimethoprim (TMP), nitrofurantoin (NIT), and chloramphenicol (CHL) in an Escherichia coli (E. coli) populace.
This uncovered enormous cell-to-cell variability in stress signal activation rate and transduction delay. Significantly, their systematic inference results recognized a formerly unrecognized parameter that causes cell-to-cell variability in light of antibiotic stress signals: the number of rate-limiting steps in the sign transduction cascade. This was surprising because countless rate-limiting steps have been known to lessen the intracellular variability in transduction delay.
The scientists’ finding of the significant sources of cell-to-cell variability in signaling dynamics is fundamental for creating more potent medications that kill all target cells, which is significant for curing cancer and numerous infectious illnesses. Their methodology gives a significant step towards elucidating cell-to-cell variability in signal dynamics, for example, in response to cytotoxic medications.
The Endpoint
In this work, the scientists developed MBI to infer cell-to-cell heterogeneity in amplified activation rate, signal transduction time, feedback inhibition time, and signal decay rate from just the time traces of the final signal response.
Specifically, without following intermediate advances experimentally, their technique could infer the number of intermediate rate-limiting steps and the time of each progression. This permitted them to classify the stress response promoters into three antibiotic stresses, namely, TET, TMP, and NIT, given the number of rate-limiting steps and the time of each step.
All through the classification, they saw that the long time delay came from either an enormous number of steps or a long time of each progression but not both. They additionally saw the counter-intuitive disparity among intracellular and cell-to-cell variability in signaling dynamics: While the intracellular variability in the transduction delay diminishes as the rate-limiting step number increases, the cell-to-cell variability doesn’t change.
Moreover, they found that as the quantity of rate-limiting steps increases, the magnitude of the cell-to-cell heterogeneity in signal activation rate, determining the strength of the signal response, increases.
This relationship is safeguarded for Poissonian-delayed birth-death cycles having any heterogeneous cell-to-cell parameter distribution, which is extendable to the non-Poissonian process with feedback regulation according to an in-silico experiment. This discovery is expected to open up new research routes into cell heterogeneity in antibiotic resistance, a critical roadblock in cancer treatment.
It would be intriguing in future work to examine whether the property can be extended to diverse systems, for example, having multimodal dynamics such as a toggle switch network with arbitrary waiting time distributions.
The deferred birth-demise process utilized in this study can depict fundamental reaction networks, like signaling cascades and mature protein synthesis. However, this model has a restriction. For example, protein dilution is displayed as a first-order reaction, and the consecutive signal activation is utilized. This could not precisely depict their contribution to extrinsic cell-to-cell variability.
To handle this, more practical, realistic dilution reflecting cell division and signal activation using a bursty reaction is required to have been joined into the delayed model as in past work. In any event, when these mechanisms are fused into the model, they could determine the formulae depicting the model dynamics. It would be interesting to utilize their framework with the formulae to systematically analyze the contribution of cell division or bursty expression to extrinsic cell-to-cell variability.
For more intricate reaction networks, moments could be inferred with Little’s Law, the Chemical Fluctuation Theorem, Wiener-Khinchin Theorem, or Lindley’s Integral Equation. In addition, a theory that converts a non-Markovian system with time delay into a topology-equivalent Markovian system by presenting an effective transition rate decoding the impact of non-Markovian processes could likewise be utilized.
Since the scientists’ technique is just in light of the low-order moments, it is computationally more effective than strategies following all individual data points. Notwithstanding, for complex frameworks, estimation utilizing low-order moments can be biased as it takes advantage of just partial information of the system. This issue could be settled by following all individual data points in the deduction, which would be intriguing in future work.
Article Source: Wook, K. D., Hyukpyo, H., & Kyoung, K. J. (2022). Systematic inference identifies a major source of heterogeneity in cell signaling dynamics: The rate-limiting step number. Science Advances, 8(11), eabl4598. https://doi.org/10.1126/sciadv.abl4598
Learn More:
Top Bioinformatics Books ↗
Learn more to get deeper insights into the field of bioinformatics.
Top Free Online Bioinformatics Courses ↗
Freely available courses to learn each and every aspect of bioinformatics.
Latest Bioinformatics Breakthroughs ↗
Stay updated with the latest discoveries in the field of bioinformatics.
Tanveen Kaur is a consulting intern at CBIRT, currently, she's pursuing post-graduation in Biotechnology from Shoolini University, Himachal Pradesh. Her interests primarily lay in researching the new advancements in the world of biotechnology and bioinformatics, having a dream of being one of the best researchers.